Algorithms 101 : From a Beginners POV

Before writing this I took a minute and remembered how I imagined myself writing algorithms for optimizing data models which fastens up the data retrieval rate would look like. But by time I grew in this field I got to know that algorithms aren’t just code. These are some of the smart ways to tackle a problem and make data work faster

As ritual I will be covering few algo topics here which I use/have used on basis of my projects, paid gigs etc. The complexity of these algorithms will rise up gradually as the blog continues.
I hope you all know what is Linear Search ?
If not no worries this is the most common technique used by algorithms to lookup for a solution to the problem, take it as searching for word in dictionary before knowing "How to search words in dictionary" going through all the pages, but its okkay if the dictionary had only 10 to 15 pages but you would need a better and optimized way when there are literally 800+ pages

Binary Search

This is a fast and efficient algorithms but only for sorted array or list, works by repeatedly dividing in the search space in half, which reduces the number of elements to check. Starting at the middle of the array, it compares the target value to middle element. If the target matches, the search is complete.
If the target is smaller, it searches the left half, if larger the right half. This process continues until the value is found

For algorithms we will be talking more about time complexity. So Binary Search's time complexity is \(O (\log n)\), making it faster than linear search for large sorted datasets

This is mainly used in searching databases, lookup tables, or implementing features like autocomplete. Here is an example of an api function which searches for a user by ID in a sorted list of users.

// Using Linear Search an going in sequential order
// it will take 10k iterations if we want to find the last user
const users = [
{ id: 1, name: "Sonita" },
{ id: 2, name: "Bonita" },
{ id: 3, name: "Aarav" },
// ... 10 thousand more more
];
function findUser(userId) {
  return users.find(user => user.id === userId); // O(n)
}

After using Binary Search Algorithm, for 10k users it just needs 14 comparisons at most to find any user

// ideal for static, sorted data like indexes or databases 
function binarySearch(users, userId) {
  let left = 0, right = users.length - 1;
  while (left <= right) {
    let mid = Math.floor((left + right) / 2);
    if (users[mid].id === userId) return users[mid];
    if (users[mid].id < userId) left = mid + 1;
    else right = mid - 1;
  }
  return null;
}

This algorithm can also be applied in client side for searching an item in a sorted dropdown list

Depth First Search

The idea of DFS is starting with the root node and go as far down one branch as possible, all the way to the end.

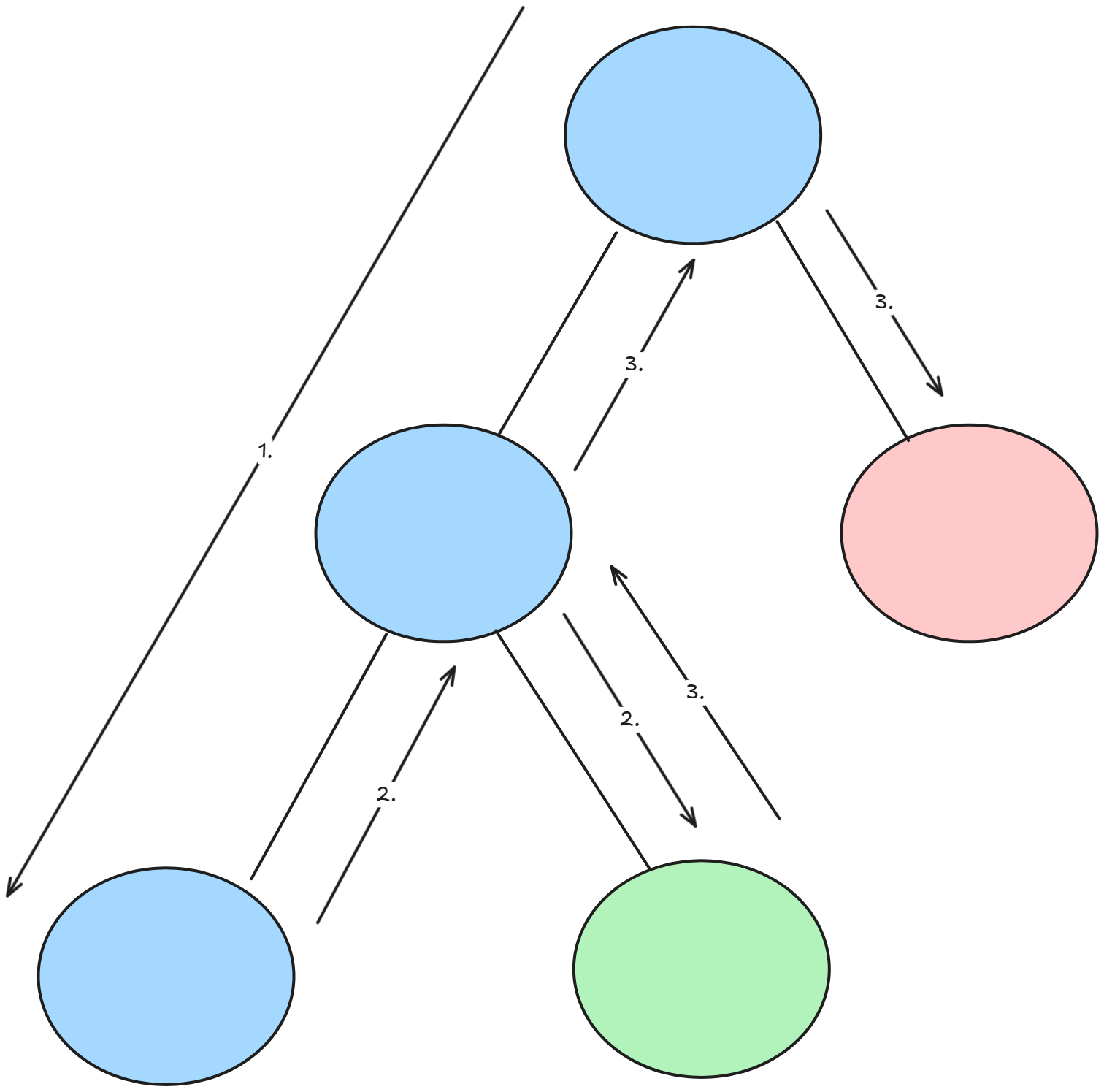
After reaching the dead end we come back to the last visited node, this process of going back to the last visited node is called Backtracking[2]. We check if there are any unvisited nodes left. If there are, we explore those nodes next. If not, we backtrack again to the previous node. This process repeats until every node in the graph or tree has been visited[3].

The time complexity of DFS depends on the graph's structure. For a graph with Vvertices (nodes) and E edges (connections), using a list of connected nodes. DFS takes \(O(V + E)\) time. This because it visits each vertex once and checks all edges to explore neighbors. It’s fast for most graphs, especially sparse ones like social networks, as it only processes the actual connections

One of the OSS issue on which I worked was related to ui rendering nested comments inefficiently with manual looping, which struggled with deep nesting

// the comments where fetched from db and stored in a list
const comments = [
  { id: 1, text: "Great!", replies: [{ id: 2, text: "Thanks!" }] },
  { id: 3, text: "Cool", replies: [] },
];
function renderComments() {
  let html = "";
  for (let comment of comments) {
    html += `
${comment.text}
`;
    if (comment.replies) {
      for (let reply of comment.replies) {
        html += `
${reply.text}
`;
      }
    }
  }
  return html;
}

My Pull request for the same issue, used DFS. I have attached the full anatomy here

//  Ideal for exploring all paths, detecting cycles, or solving problems requiring exhaustive search.

// "comments" is an array of comment objects
// "deep" is an optional parameter indicating how deep in the reply
// hierarchy we are, will be starting at 0 (top-comment)
function renderComments(comments, depth = 0) {
  // this will hold the final html output that gets
  // returned
  let html = "";
  // helps in iterating through each comment
  for (let comment of comments) {
    // appending the current comment's text to
    // the html string
    "html += `${comment.text}`;"

    // using recursion here
    if (comment.replies) {

      // if the comment has replies 'comment.replies' exits, then recursively renderComments
      // on those replies
      // and increase the depth by 1 to indicate you are now
      // rendering a deeper level of replies
      html += renderCommentsDFS(comment.replies, depth + 1);
    }
  }
  return html;
}

This can also be used for detecting cycles in dependency graphs for building package managers.

Breadth First Search

In Breadth first search it explores graphs differently. Instead of diving deep like DFS, BFS visits all nodes at the current "level" before moving to next.

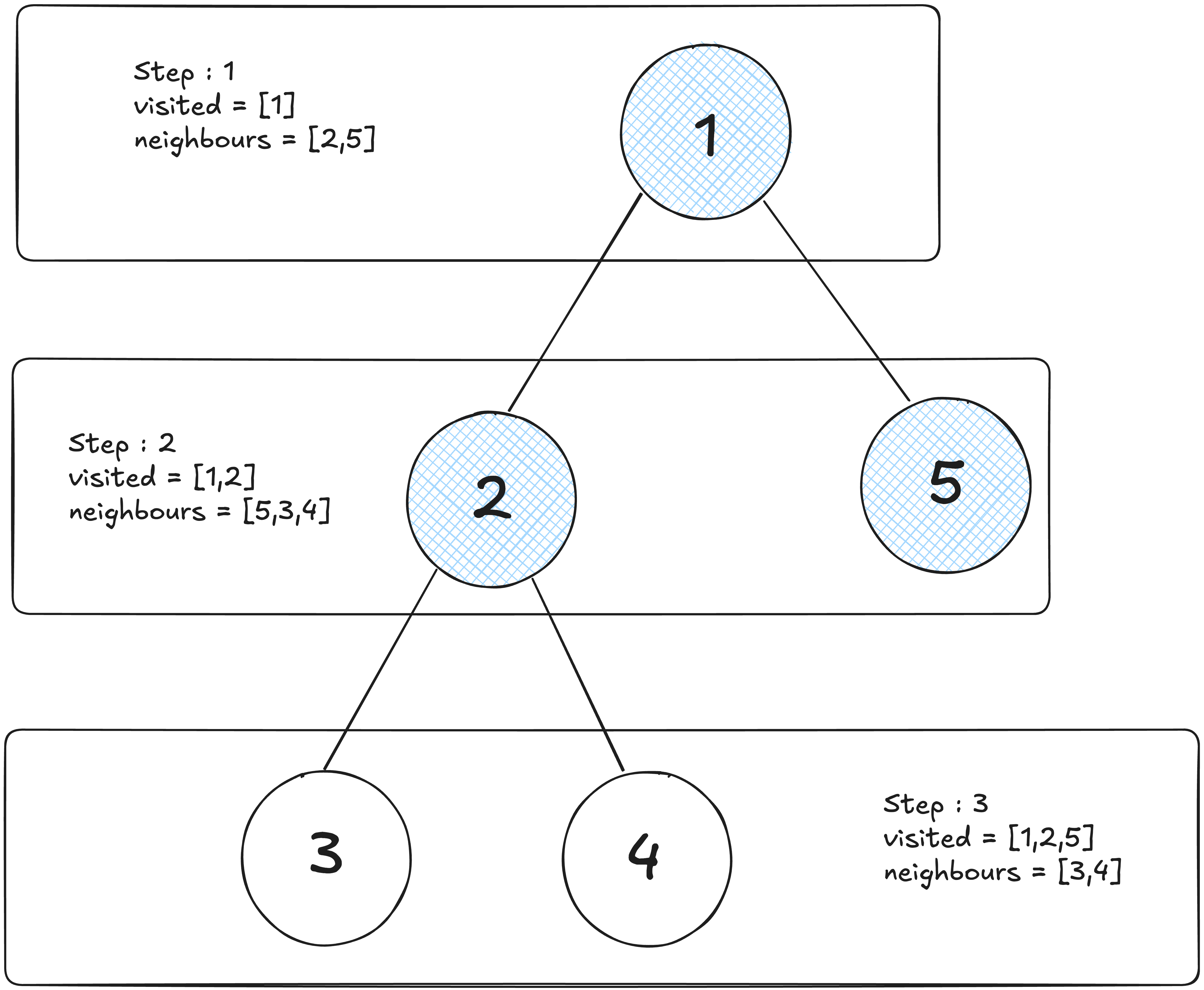
Starting from a chosen node, it explores all its immediate neighbors first, then their neighbors, and so on. This makes BFS ideal for finding the shortest path in unweighted graphs for exploring nodes closer to starting point.

For the time complexity part we can say its similar to DFS which is \(O (V + E) \) but the only difference is, BFS uses queue to track nodes, ensuring it explores closer nodes first, which is why its great for finding shortest paths in unweighted graphs, like in navigation apps or GPS

Code Dissection of Friends graph is written below

const users = {
  'Sonita': ['Aarav', 'Charlie'],
  'Bonita': ['Vegeta', 'David'],
  'Gojita': ['Vegito'],
  'Majin Buu': ['Mr. Satan']
};

function findConnection(user1, user2) {
  // starting with user1 with a connection distance of 0
  const queue = [[user1, 0]];
  // this const keeps track and avoids revisiting
  const visited = new Set([user1]);

  // this is the main loop for BFS
  while (queue.length) {
    // taking the front node using 'shift()' is used because it's a
    // queue, 'user' is the current person being explored
    // distance is how many steps away this user is from user1
    const [user, distance] = queue.shift();

    // if the current user is the target, return the distance
    // this also shows no.of steps needed to get from user1 to user2
    if (user === user2) return distance;

    // for every friend of current user
    // if we haven't seen this friend before
    // mark them as visited
    // add them to queue with an updated distance (distance + 1) 
    // one more step away from user1
    for (let friend of users[user]) {
      if (!visited.has(friend)) {
        visited.add(friend);
        queue.push([friend, distance + 1]);
      }
    }
  }

  // if loop finishes without any friends
  // than we return -1 means (not found)
  return -1;
}

Insertion Sort Algorithm

Insertion sort is a simple sorting algorithm that builds a sorted array one element at a time.

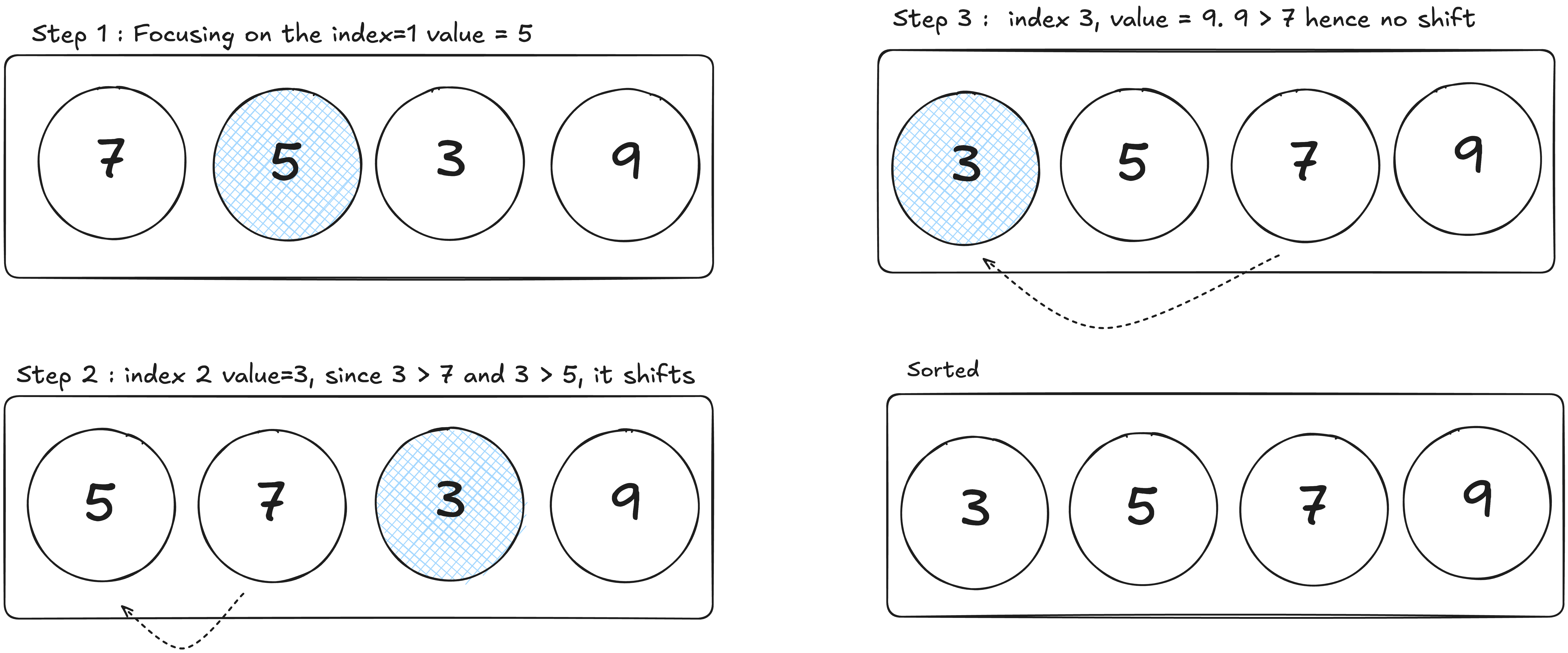
Starting with the second element, insertion sort compares it to the previous ones, shifting larger elements right until it finds the right spot to "insert" the element. This process repeats for each element until the entire array is sorted. Works well for small datasets or nearly sorted lists, like organizing a short list of names or numbers.

The time complexity of Insertion Sort depends on the array size and its initial order. For an array with n elements, the worst-case time complexity is \(O(n^2)\), as each element may need to be compared and shifted against all previous elements, like when the array is reverse-sorted. In the best case, such as a nearly sorted array, it runs in \(O(n)\) time, as each element requires minimal comparisons and shifts. This makes Insertion Sort efficient for small or nearly sorted datasets but less ideal for large, unsorted lists compared to faster algorithms like Quick Sort.

We can code a Search history using insertion sort

function insertionSort(arr) {
  // Start from the second element (i = 1), since the first element is considered "sorted"
  for (let i = 1; i < arr.length; i++) {
    
    // 'key' is the current element we want to insert into the sorted part of the array
    let key = arr[i];

    // 'j' marks the end of the sorted portion (just before the current element)
    let j = i - 1;

    // Move elements of arr[0..i-1], that are less than 'key.time', one position ahead
    // We sort in descending order based on 'time' property
    while (j >= 0 && arr[j].time < key.time) {
      // Shift the element to the right
      arr[j + 1] = arr[j];
      j--; // Move one step back in the array
    }

    // Insert the 'key' in its correct position
    arr[j + 1] = key;
  }

  // Return the sorted array
  return arr;
}

Merge Sort Algorithm

Its a reliable sorting algorithm which uses a divide and conquer approach to sort arrays efficiently.

It works by splitting the array into two halves, sorting each half recursively, and then merging the sorted halves back together to create a fully sorted array. Its stable meaning, it preserves the relative order of equal elements, and is ideal for large datasets, like sorting customer records or database entries, due to its consistent performance.

Lets talk a little about the time complexity here, merge sort has a time complexity of \(O(n log n)\) in all cases from best, average to worst. For example lets take the above figure which is [4, 2, 5, 1, 8, 3, 7, 6] here \(n=8\) elements and for \(n=8\), it takes \(log_2 8 = 3\) levels of division (8 -> 4 pairs -> 2 groups of 4 -> 1 group of 8). Our figure starts with four groups of two, which is part of this process

At each level, all \(n\) elements are merged. Merging two sorted lists compares and combines elements in linear time. Merging four pairs \(([4, 2], [5, 1], [8, 3], [7, 6])\) into two groups takes about 8 comparisons total. Merging two groups \(([1, 2, 4, 5], [3, 6, 7, 8])\) into one takes another 8 comparisons
The O(n log n) complexity holds because the number of divisions is logarithmic \(log n \), and each merge step scales linearly with \(n \). Unlike Insertion Sort's \(O(n^2)\) (upto 64 operations for n = 8)

Before
The API gets session data from the DB. Uses .sort() which may be unstable or optimized differently depending on V8 engine. So we get less control over performance in large datasets

// routes/sessionStats.js
app.get('/api/sessions/sorted', async (req, res) => {
  const sessions = await db.getUserSessions(); // returns array like [120, 30, 45, 60]
  
  // Using built-in sort (not always stable or predictable)
  const sorted = sessions.sort((a, b) => a - b);

  res.json({ sorted });
});

After using Merge Sort
After using our own implementation of merge sort and replacing it with built-in sort, it helped with performance tuning and custom rules which can handling large logs or preprocessing logs offline

// utils/mergeSort.js
function mergeSort(arr) {
  if (arr.length <= 1) return arr;

  const mid = Math.floor(arr.length / 2);
  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));

  return merge(left, right);
}

function merge(left, right) {
  const result = [];
  let i = 0, j = 0;

  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) result.push(left[i++]);
    else result.push(right[j++]);
  }

  return result.concat(left.slice(i)).concat(right.slice(j));
}

module.exports = { mergeSort };


// on different file we can call the function and use it
const { mergeSort } = require('../utils/mergeSort');

app.get('/api/sessions/sorted', async (req, res) => {
  const sessions = await db.getUserSessions();

  const sorted = mergeSort(sessions);

  res.json({ sorted });
});

Quick Sort Algorithm

This uses the same strategy as Merge Sort algorithm which is divide and conquer strategy to sort arrays. But it works by picking a "pivot" element, partitioning the array so that element smaller than the pivot are on its left and larger ones on its right, then recursively sorting the left and right sub-arrays.

Quick Sort is fast and widely used for large datasets, like sorting student grades or product lists, due to its average-case speed.

For an array with n elements, Quick Sort’s time complexity is \(O (n log n)\) on average, making it very fast for most cases. It divides the array into two parts around a pivot, ideally halving the problem size each time, requiring log n levels and n comparisons per level. sorting an array of 8 elements takes about 24 operations (8 * log 8). In the worst case, like a sorted or reverse-sorted array with a poor pivot choice, it can degrade to O(n²), but this is rare with good pivot strategies.

Choosing a good pivot is crucial for efficiency, as it effects how evenly the array is split. Here are some common steps you can include while choosing one :

• First / Last Element: Pick the first or last element, but this can lead to \(O(n^2)\) time in sorted or reverse-sorted average performance.
• Random Pivot : Select a random element to reduce the chance of worst-case scenarios, improving average performance. But how you would ask. Choosing a random pivot in quick sort increases avg. performance by reducing the likelihood of consistently poor partitions, which can lead to worst-case \(O(n^2)\) time complexity.When a pivot is randomly selected from the array, it’s unlikely to repeatedly pick the smallest or largest element, as happens in sorted or nearly sorted arrays with fixed pivots (e.g., first element). Instead, random pivots tend to create more balanced partitions, splitting the array closer to half each time, which aligns with the ideal \(O(n log n)\) average-case performance. For example, in \([4, 3, 5, 2, 6, 1, 7, 8]\), a random pivot like 5 might split into [4, 3, 2, 1] and [6, 7, 8], keeping sub-arrays roughly equal. This randomness averages out bad cases over many runs, ensuring partitions are balanced more often, with each level taking O(n) comparisons across log n levels.

Before
The best way I learned quick sort algorithm was by implementing it in a e-commerce api in which products were sorted by price, at first I thought using .sort() would be but NVM XDD. It was simple and short but lacked control and it can't handle complex logic lick preprocessing, side effects, or tracing steps for debugging

// routes/products.js
app.get('/api/products/sorted', async (req, res) => {
  const products = await db.getProducts(); // [{ name: "Shoes", price: 80 }, ...]

  const sorted = products.sort((a, b) => a.price - b.price);

  res.json({ sorted });
});

After
After learning and implementing my own Quick Sort to sort products by price, this let me add debug logs, skip invalid prices, add thresholds or filtering inline, or customize order (ascending / descending)

function quickSortProducts(arr, ascending = true) {
  if (arr.length <= 1) return arr;

  const pivot = arr[arr.length - 1];
  const left = [];
  const right = [];

  for (let i = 0; i < arr.length - 1; i++) {
    if (!arr[i].price) continue; // skip if price is missing

    if (ascending ? arr[i].price < pivot.price : arr[i].price > pivot.price) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }

  return [
    ...quickSortProducts(left, ascending),
    pivot,
    ...quickSortProducts(right, ascending),
  ];
}

module.exports = { quickSortProducts };

const { quickSortProducts } = require('../utils/quickSortProducts');

app.get('/api/products/sorted', async (req, res) => {
  const products = await db.getProducts();

  const order = req.query.order || 'asc'; // ?order=desc
  const sorted = quickSortProducts(products, order === 'asc');

  res.json({ sorted });
});

I wanted to add greedy algorithm and DP but that would be an overkill for this blog, these are searching and sorting algorithms which is mainly used during development
Hope I was able to add few value to your today's learning :)